The Linear Algebra Notes

4,052次阅读

This is an outdated article of the linear algebra notes.

Please check the new version here: https://blog.lyzen.cn/2023/07/10/The-Linear-Algebra-Notes/

This notes is about the fundamental of Linear Algebra lectured by MIT-1806.

You can right-click formulas to check their $\LaTeX$ codes or left-click pictures or animations to check their python codes which depend on matplotlib and manim.

If the LaTeX formulae cannot be displayed correctly, try refreshing the page.

Some media are from the Internet. You can find them in reference.

Here are wonderful resources which is useful for learning linear algebra:

Essence of linear algebra by 3Blue1Brown [Official | Youtube | Chinese translation on bilibili]

The fundamental problem of linear algebra is to solve a system of linear equations.
The normal case is n equations with n unknowns. For example:

$$\begin{cases}\ 2x&-y&=0 \\ -x&+2y&=3\end{cases}$$We can use matrix and vector to express it:$$\begin{equation}\begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} =\begin{bmatrix} 0 \\ 3 \end{bmatrix}\end{equation}$$Using three letters to express this three matrix:$$ A\mathbf{X}=b $$A is coefficient matrix. $X$ is vector of unknowns. $b$ is vector of the right-hand numbers of equations.

We can draw the row pictures of equations on a xy plane. Obviously They are two lines. all the points in each line are solutions of equation.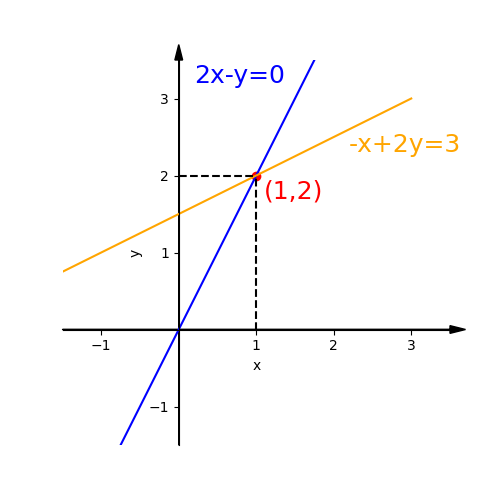

Then the column pitures：
Focusing on the columns of matrix, we can get this:$$\begin{equation}x \begin{bmatrix} 2 \\ -1 \end{bmatrix} + y\begin{bmatrix} -1 \\ 2 \end{bmatrix} =\begin{bmatrix} 0 \\ 3 \end{bmatrix}\end{equation}$$

This equation is asking us to find the x and y to combine the vector $x\begin{bmatrix} 2 \\ -1 \end{bmatrix}$ and the vector $y\begin{bmatrix} -1 \\ 2 \end{bmatrix}$ to get the vector $\begin{bmatrix} 0 \\ 3 \end{bmatrix}$. That is the linear combination we need to find.

Draw three vectors mentioned above. We already know the right x and y. So we can get the red vector when combining 2 green vectors and 1 blue vector.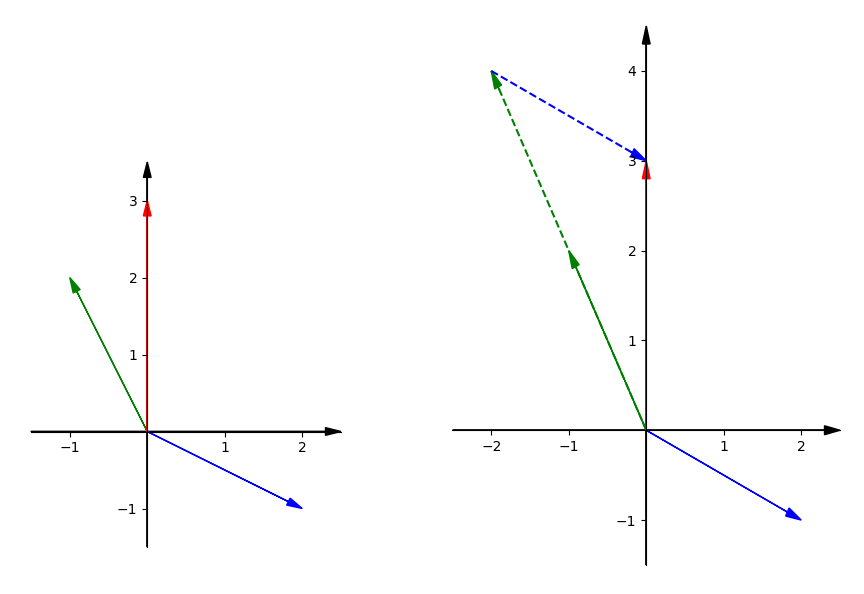

If we change the x and y, we can find that the new vector is able to fill all the xy plane. It means we can produce a vector point at everywhere in this plane.

Now let’s see the 3×3 case.$$\begin{cases}2x & -y & &= 0 \\-x & +2y & -z &= -1 \\& -3y & +4z &= 4\end{cases}$$

Similarly, We can use $ A\mathbf{X}=b $ to describe it.$$\begin{equation}A=\begin{bmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -3 & 4 \end{bmatrix},\mathbf{X}=\begin{bmatrix} x \\ y \\ z \end{bmatrix},b=\begin{bmatrix} 0 \\ -1 \\ 4 \end{bmatrix}\end{equation}$$

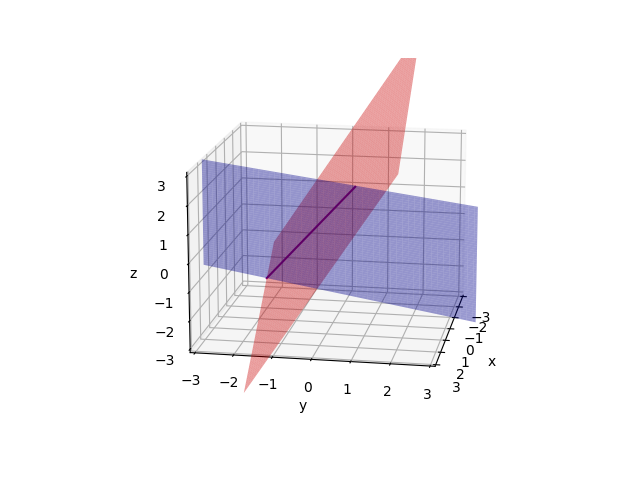
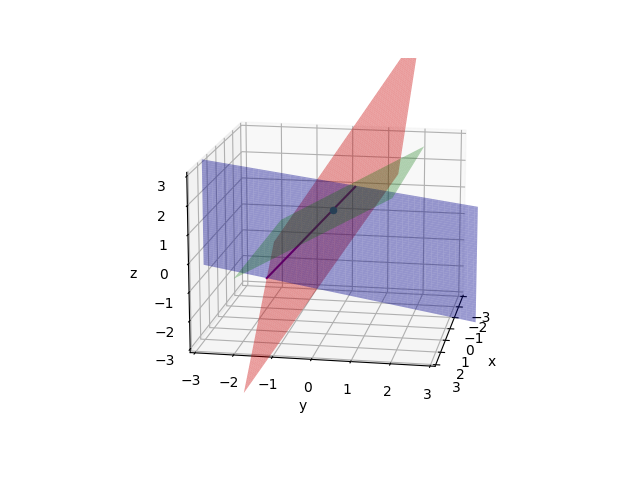
See the row pictures:Firstly draw two planes(2x-y=0 and -x+2y-z=-1). These planes meet in a line.

Then draw the third plane(-3y+4z=4).They meet in a point(0, 0, 1). And this point is solution of equations.

This row picture is complicated. In 4×4 case or higher dimensions, the problem will be more complex and we cannot draw a picture like this.

Those three planes are not parallel, and they are not special.

Then column pictures:$$\begin{equation}x \begin{bmatrix} 2 \\ -1 \\ 0 \end{bmatrix} +y \begin{bmatrix} -1 \\ 2 \\ -3 \end{bmatrix} +z \begin{bmatrix} 0 \\ -1 \\ 4 \end{bmatrix} =\begin{bmatrix} 0 \\ -1 \\ 4 \end{bmatrix}\end{equation}$$

Solve this equation so we can get the linear combination of three vectors. Each vector is a three dimensions one.

Then we can get $x=0, y=0, z=1$.

If we change the $b$. For example $b = x\begin{bmatrix} 1 \\ 1 \\ -3 \end{bmatrix}$. We can also get the linear combination $x=1, y=1, z=0$.

Think about this:
Can I solve $A\mathbf{X}=b$ for every $b$?

If we change the x, y and z in this example, we can find that the new vector produced can point at everywhere in this space.

So in linear combination words, the problem is

Do the linear combinations of the columns fill three dimensional space?

In this example, for the matrix $A$, the answer is yes.

Imagine that if three vectors are in the same plane, and the vector $b$ is out of this plane. Then the combination of three vectors is impossible to produce $b$. In this case, $A$ is called singular matrix. And $A$ would be not invertible.

Column operation: $\begin{equation}\begin{bmatrix} a & b \\ c & e \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} =x\begin{bmatrix} a \\ c \end{bmatrix} +y\begin{bmatrix} b \\ d \end{bmatrix}\end{equation}$

See what happens to $\begin{equation}\begin{bmatrix} \color{green}3 & \color{red}1 \\ \color{green}1 & \color{red}2 \end{bmatrix}\begin{bmatrix} \color{orange}-1 \\ \color{orange}2 \end{bmatrix} =\begin{bmatrix} \color{orange}-1 \\ \color{orange}3 \end{bmatrix}\end{equation}$